こんにちは、四谷学院スタッフの山中です。
9月15日に書かれた、現役高校生らしき方の「logなんて必要ねぇんだよ!」というツイートが、いいね約12万、リツイート約5万3千(9月20日時点)という爆発的なバズり方をしていました。
(実際のツイートはこちら)。

そこで、今日は四谷学院が誇る数学のK先生に、このlogの話について学習アドバイスをいただきました。
「logなんていらない」というあなたに。
内容はというと、テストで出題された
3の30乗は何桁の数か。
という問いに対して、実際に3の30乗を計算して「15桁」と解答し、ちゃんと○をもらった、という写真に上記のセリフが添えられていたものです。なお、問題文には
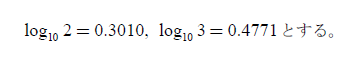
という但し書きがついています。
先に、出題した先生が期待している模範的な解答を書いておくと、
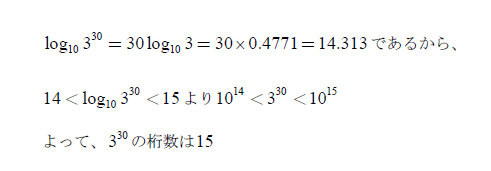
といった感じになるでしょう。
これに対する件の投稿者さんの解答を写すと、

というもので、実は私、こういう力づくな解答はけっこう嫌いじゃないです
ともかく、実際に3m³0;を計算しようと思ったときに、
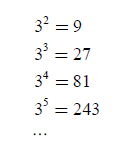
と順番に3を30個かけるのではなく、ちゃんと2個ずつまとめて「多少なりとも計算を工夫しよう」と思っているところがエライ。

ただ惜しむらくは、最後の最後で計算が間違っていて
43046721 × 4782969 = 205891132094649
が3の30乗の正しい値であったところ。
もし私が採点者であったらば計算を確認して(もちろん電卓ソフトで)、「計算が違うから0点」としていたでしょうね。
ここで、
43046721 × 4782969
まででたら、求めたいのは3の30乗の正確な値ではなく桁数なのだから、ということで
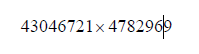
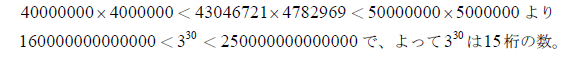
とすればラクなのですが、ここまできたらラクとかどうとかじゃなくて、このまま強行突破したくなるのが人情、というものでしょう。
そんなことない?
「log」考え方のコツ
それはともかく、なぜ私がこの解答に好感をもつかというと、そもそもこの手の問題の
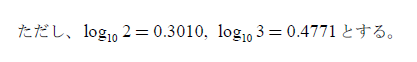
に対して「どうしてそんなことわかるんだよ」と思ってほしいなあ、という気持ちが心の奥のほうにあるからだと思います。
みなさんはそんなこと考えたことないですか?
細かい値はちょっとわきに置いて先に大雑把なはなしをします。2の10乗=1024は覚えておいて損のない数字で、実生活でも「1ギガバイト=1024メガバイト」は知っている人も多いでしょう。これを、
![]()
と思うことにすれば、
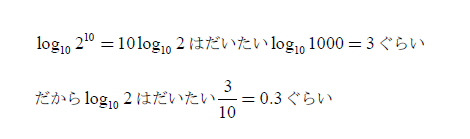
と思うことができるわけです。
この「だいたい」の数値ををもっと正確にしようと思うと、

ということになるわけです。
ここで
![]()
ということを認めていただければ、
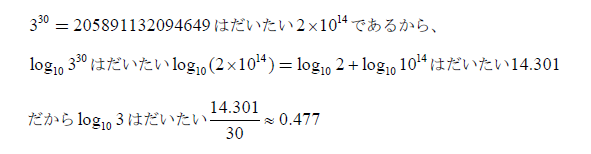
もちろん計算の工夫はさまざまに行なうのですが、基本の考えとしては適当なnに対して3のn乗がだいたいどれくらい、という計算から log103の値が求まってくるわけで「実際に3の30乗を計算する」ことは対数計算の本筋に迫っている、と言えないこともないのです(ちょっと強引だけど)。
もともと対数は大航海時代に生まれたもので、ざっくりいうと巨大な数どうしのかけ算
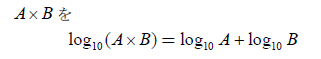
と足し算を経由することで計算しようとするものでした。
そのために、
![]()
といった具体的な値をまとめた「対数表」がつくられたのであり、件のツイートはその歴史に寄り添っている、と言えないこともないのです(強引すぎだけど)。

こうやって考えてみると、数学も面白くなってきますよね。



